Nom : ...................... Prénom : ...........................

Contrôle - Dérivation

Exercice 1 On considère la fonction $g$ définie sur $]0;\infty[$ par $g (x) = \frac{1}{x} - x + 3$. On note $C_g$ sa courbe représentative.

1 Calculer la fonction dérivée $g' (x)$.

2 Calculer $g (2)$ et $g'(2)$.

3 Quelle est le coefficient directeur de la tangente à $C_g$ au point d`'abscisse $1$ ?

Exercice 2 On considère la fonction d'équation $f (x) = x^3 - 2x^2 - x$ représentée ci-dessous :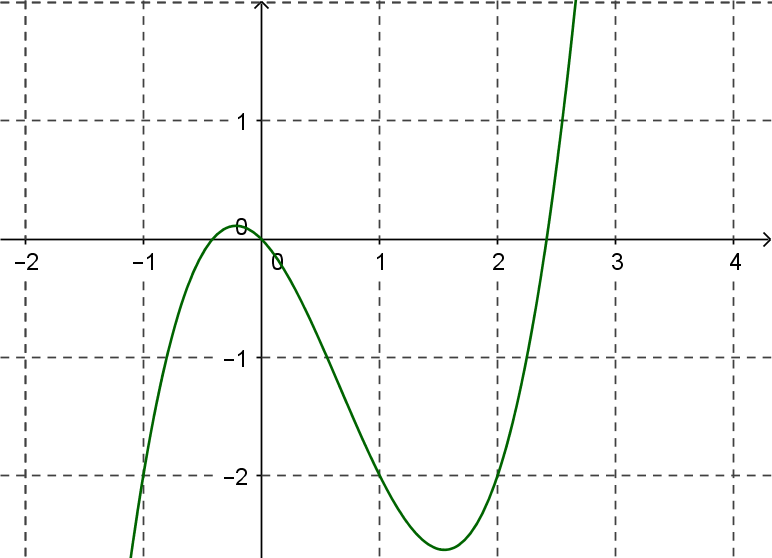

1 Calculer la dérivée $f'(x)$.

2 Calculer $f'(2)$ et tracer sur le graphique la tangente au point d'abscisse $2$

Exercice 3 On étudie une l'évolution d'une population de bactérie pendant 12 heures. On note $t=0$ l'instant initial et $t=12$ l'instant final. $t$ est exprimé en heures. On note $f (t)$ le nombre de bactéries présentes à l'instant $t$. L'étude est représentée par le graphique ci-dessous :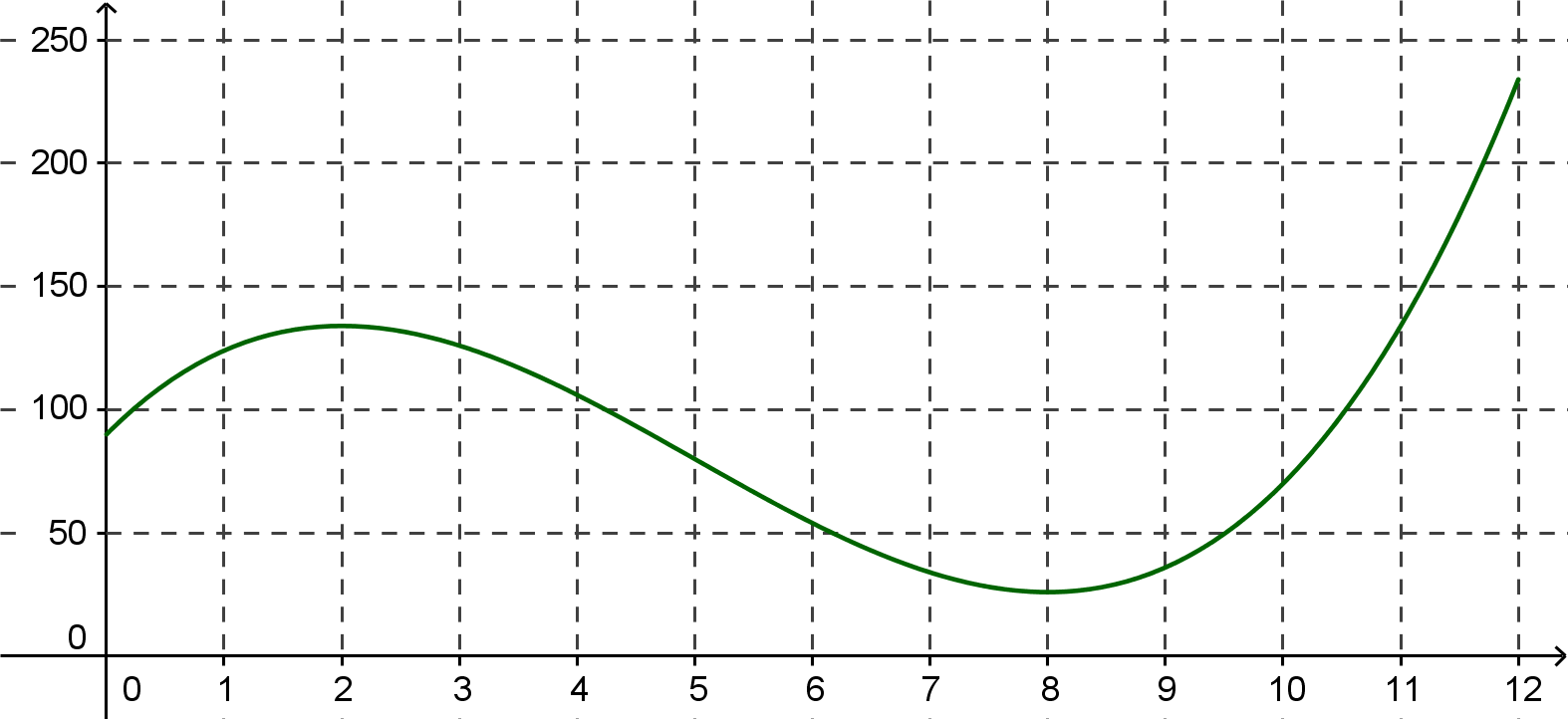

AEtude graphique

1 Quel est le nombre de bactéries initial ?

2 Quel est le nombre de bactérie au bout de 12 heures ?

3 Quel est le nombre minimal de bactéries et à quel instant est-il atteint ? Même question pour le nombre maximal.

BEtude théorique

On admet que la fonction \est définie par l'équation $f (t) = t^3 - 15 t^2 + 48 t + 90$ pour $t$ dans $[0;12]$

1 Calculer la dérivée $f'(t)$

2 Montrer que $f'(t)=3 (t-2) (t-8)$

3 En déduire le tableau de variations de la fonction $f$

4 Confirmer les observations de la question A.3

Correction

Exercice 1 $g (x) = \frac{1}{x} - x + 3$ définie sur $]0;\infty[$

1 $g' (x) = \frac{-1}{x^2} - 1$

2 $g (2) = \frac{1}{2} - 2 + 3 = 1,5$ et $g'(2) = \frac{-1}{2^2} - 1 = -2,25$.

3 Le coefficient directeur de la tangente à $C_g$ au point d`'abscisse $1$ est $g'(1) = \frac{-1}{1^2} - 1 = -2$

Exercice 2 Soit $f (x) = x^3 - 2x^2 - x$ définie sur $\mathbb{R}$ :

1 $f'(x) = 3 x^2 - 2\times 2 x - 1 = 3 x^2 - 4 x - 1$

2 $f'(2) = 3\times 2^2 - 4 \times 2 - 1 = 3$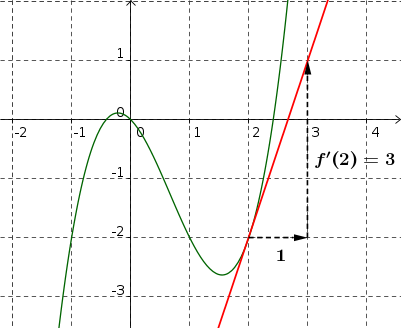

Exercice 3

AEtude graphique

1 Le nombre de bactéries initial $f (0)$ vaut environ $90$

2 Le nombre de bactéries final $f (12)$ vaut environ $230$

3 Le nombre de bactéries minimal vaut environ $25$ (atteint au bout de $8$h ) et le nombre maximal vaut environ $230$ (atteint au bout des $12$h )

BEtude théorique

Soit $f (t) = t^3 - 15 t^2 + 48 t + 90$ pour $t$ dans $[0;12]$

1 $ \begin{array}{lll} f'(x) &=& 3 t^2 - 15\times 2 t + 46 \times 1 + 0 \\ &=& 3 t^2 - 30 t + 46 \\ \end{array} $

2 On développe $3 (t-2) (t-8)$ : $$ \begin{array}{lll} 3 (t-2) (t-8) &=& (3t-6) (t-8) \\ &=& 3 t \times t - 3 t\times 8 - 6 \times t -6\times (-8) \\ &=& 3 t^2 - 24 t - 6 t + 48 \\ &=& 3 t^2 - 30 t + 48 \\ &=& f (t) \\ \end{array} $$

3 $t - 2$ s'annule en $2$ et $t - 8$ s'annule en $8$ $$ \begin{array}{c|lcccr|} x & 0 & & 2 & & 8 & & 12 \\ \hline t-2 & & - & |\hspace{-0.15cm}0 & + & & + & \\ \hline t-8 & & - & - & - & |\hspace{-0.15cm}0 & + & \\ \hline f' (x) & & + & |\hspace{-0.15cm}0 & - & |\hspace{-0.15cm}0 & + & \\ \hline f (x) & f (0) & \nearrow & f (2) & \searrow & f (8) & \nearrow & f (12) \\ \hline \end{array} $$

4 $f (0) = 90$ , $f (2) = 134$, $f (8)=26$ et $f (12) = 234$. Le tableau de variation confirme donc la question A.3